Day 7: (Continued Story) the Paradox

For the continued story of contradiction, this time I'd like to introduce you something more exciting, it's called--Paradox, which is more fascinating to me, and it leads to uncoordinated contradictions. So first we need to know the difference and connection between paradox and contradiction. Generally, a contradiction is a statement that contains more than one propositions which cannot be all true at the same time, the solution is you have to discard some of them. While paradox is a statement that can neither be true nor false for both of the situation would lead to contradictions and there is no solution to fix it.

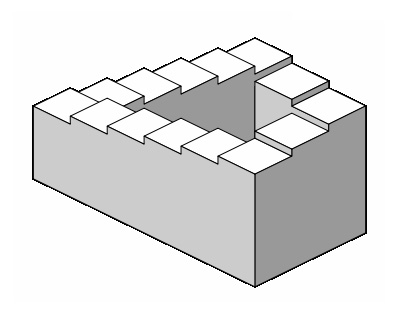Penrose Stairs. It never ends. (photo source)

By the explanation above, it is easy to see that the example in the former blog entry is a contradiction, because the announcement "I’m not going to post today" and the fact that "I posted it at last" (stated in another way) cannot be all true at the same time. There are also some similar contradictions stated as "I'm not typing on a computer", "I'm saying nothing", "The color of these words is red"...and so on.

When it comes to paradox, the most famous and simplest example is liar paradox which stated as "This statement is false". It is a paradox because if it's true, then the statement is false, contradiction; if it's false, then the statement is true, another contradiction. So the statement can neither be true nor false. There are also some other famous paradoxes shown as below. 

1. Barber paradox from Russell, stated as "Who is going to shave the barber who only shaves those men who don't shave themselves?"

2. "Is the answer to this question no?"

3. "The following sentence is true", "The previous sentence is false"

                                .......(see more here).......

The statements above all turn out to be paradoxes as we expected, then the following questions come up naturally: How could a statement can neither be true nor false? What goes wrong? And does it mean our logical is not reliable? What is the contribution to come up with those paradoxes?

All of these paradoxes above generate contradictions by self-referencing. Let's keep our attention on the liar paradox, let proposition P="this statement is false", since "this statement" stands for P, therefore, we have P="P is false", then you can see it can be stated in a ridiculous way "P is true when P is false". My dear readers, if you were interested to the rest paradoxes, you could get the same results like "P is something that P is not". And the arbitrary usage of language is all the reason that miseries start!!! 

Our logical is still well-functioning, and soon you will see the tremendous significance of the discovery of paradoxes. When "P is something that P is not" was translated into set language, that is: P={x|x doesn't belong to P}, and other paradoxes can be also translated into such kind of set language. So, does such kind of sets like P exist? As we all know, in the early time the elements of a set were defined by describe words without much limits, but after these "sets" were being found, they even lead to the Third Mathematical Crises! To kick these paradox "monsters" out of logical world, the mathematicians spent years to find the axioms and build modern logic and set theory which are the foundation of everything!

Barber Paradox can be translate into set language: Could a set belong to itself? (photo source)

Another interesting result can be deduced from a paradox known as The Grandfather Paradox, it shows that if time traveling is possible, then parallel universes may exist and we are living in one of them! There also many interesting paradox in other areas such as geometry and physics.

If time traveling is possible, to deal with the Grandfather Paradox, then Parallel universes could be exist! (photo source)

Okay, I think that's it for today's blog entry! This time I talked a lot about math and logic, hope it won't be boring for you:-) I really like this topic because it is so fascinating, important and it's also part of my searching. As there was a saying that logical is the way how God thinks!